Polyhedral Structures
Polyhedra - solids formed from plane parts - play an important role in manufacturing from plane materials. Plato had already described the five possible completely regular solids and assigned them to the elements. Kepler studied polyhedral structures in his world harmonics, used them to create dense space packings and to describe planetary orbits. The starting point of our seminar were considerations on (semi-)regular polyhedra. The principle of duality proves to be an effective geometric tool for moving from semi-regular polyhedra to polyhedra formed from identical but irregular polygons.
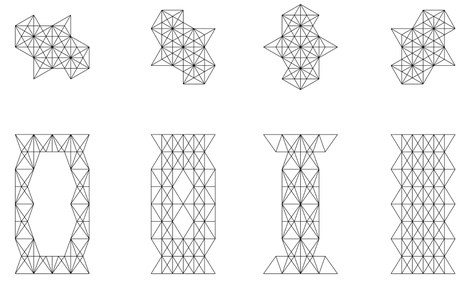
Arutiun Papikian dealt with polyhedral supporting structures. After studying the approaches of Richard Buckminster Fuller and Konrad Wachsmann, he developed a triangular supporting structure out of irregular polyhedra, calling it the Ж-structure. It is supposed to be able to be used horizontally, vertically and laterally due to its geometric order. Viewed from different angles, the manifold possibilities of this polyhedral structure become clear.

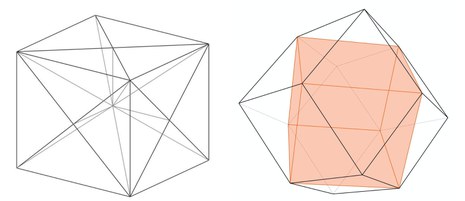
Philipp Lorenz succeeded in turning the cube upside down by dividing it into equal parts. He divided the cube into congruent tetrahedra and joined these 24 links together in a joint ring. The Cube X developed by Fred Voss in 2006 thus became the Cube X2 by further subdividing each side of the cube by means of two surface diagonals. When the cube is inverted into a rhombic dodecahedron with an internal hollow space in the shape of the cube, many intermediate stations are possible as shape variations.


