Pattern Matters
Dozentinnen: Akad. Dir. Cornelie Leopold, Dipl.-Ing. Viyaleta Zhurava

Die Auseinandersetzung mit Patterns ist Grundlage für viele Gestaltungsaufgaben. Wir wählten das englische Wort Pattern, da dieses besser als Muster, Flächenornament, Parkettierung, Anordnungen ... diese verschiedenen Aspekte umfasst. Parkettierung meint die lückenlose und überlappungsfreie Überdeckung kongruenter Figuren, die ausgehend von geometrischen Grundformen auch figurativ werden können. Raumpackungen sind das räumliche Pendant der ebenen Muster. 3D-Packungen mittels Polyeder bilden die Basis für räumliche Anordnungen und Kompositionen. Durch Transformationen und Metamorphosen sind Übergänge zwischen den Patterns und räumlichen Kompositionen möglich. Dadurch können auch Gestaltungsprozesse von regelmäßigen zu unregelmäßigen Mustern vermittelt werden.


In der Architektur wird vom Städtebau über Gebäudestruktur bis Tragstruktur auf diese geometrischen Zusammenhänge aufgebaut. Daher analysierten wir auch entsprechende Architekturbeispiele.


Aus 2D- und 3D-Patterns sowie deren Transformationen bzw. Metamorphosen entstanden die studentischen Pattern Matters Projekte als digitale und materialisierte Komposition.


Das Arbeiten mit der 3D-Modellierungs-Software Rhinoceros wurde als geeignetes Werkzeug genutzt. In einer freiwilligen Blockveranstaltung mit Eva Hagen vor Semesterbeginn bekamen die Studierenden hierzu Grundlagen vermittelt bzw. Fortgeschrittene erhielten erweiterten Input. Es wurde auch parametrisches Entwerfen mittels Grasshopper integriert.
Gastvortrag
Architekt - Univ. Lektor
Ornamental Art & Design, Wien
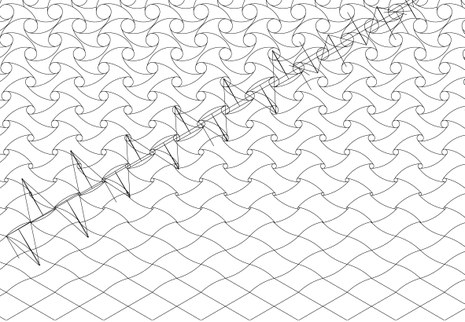
Design and Analysis of Parquet Deformations
Dienstag, 04. Mai 2021, 10 Uhr
Workshop
Ph.D. Researcher in the Centre for Studies of Architecture and Urbanism, Faculty of Architecture, University of Porto, Portugal
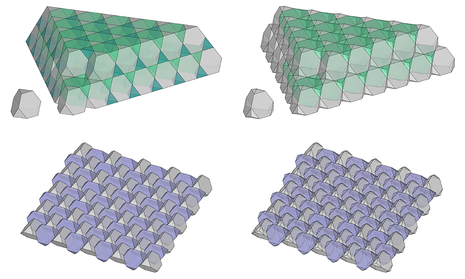
Tessellating and Interlocking in Patterns
Dienstag, 18. Mai 2021, 10 Uhr
Having understood the connections between 2D and 3D tessellations, we addressed the concept of topological interlocking and learned how the interlocked assemblies of convex regular polyhedra are obtained.
With the knowledge of some basic rules, the participants then were able to model, on their own, interesting patterns with tessellated or interlocked polyhedra.

